Skattningsskalornas statistik

Rekommenderad läsning före denna webbsida	Vad du får ut av att läsa denna webbsida
Introduction till statistik Observationer och variabler Att välja statistisk metod	Skattningsskalornas statistik kan först tyckas invecklad. När du läst den här webbsidan ett par gånger inser du att det svåra är inte att hitta den rätta regeln (för den finns inte) utan att hitta ett rimligt alternativ som passar dina behov och sedan hitta argumenten för att kunna försvara det du gör.

Introduktion till skattningsskalor

På en vårdcentral i den stora staden Gröteborg arbetar dr Citron. Han heter egentligen något annat men på grund av sitt stora intresse för C-vitamin kallar både personal och hans patienter honom för dr Citron. Han har haft flera patienter som har berättat att de mått bättre efter att ha börjat med C-vitamin. Nu vill dr Citron på ett vetenskapligt sätt undersöka om människor upplever att de får en bättre hälsa och livskvalitet om de börjar äta C-vitamin. Han är i den här studien mer intresserad av människors upplevelser än om man kan se faktiska ändringar i blodtryck, kolesterol etc. Dr Citron väljer att mäta upplevd hälsa med en enkät omfattande en eller flera frågor. Hur skall han göra rent praktiskt? Låt oss återkomma till dr Citron och hans projekt.

Enkäter kan ha öppna frågor där den som svarar skall berätta fritt. Alternativet till öppna frågor är slutna frågor med fördefinierade svarsalternativ. Här finns två varianter. Den ena är svarsalternativ utan inbördes ordning och resultaten mäts då enligt en nominalskala. Andra alternativet är följaktligen svarsalternativ med inbördes ordning och de mäts då med ordinalskala. Sistnämnda innebär någon form av gradering och kallas allmänt för skattningsskala. Resten av den här webbsidan diskuterar bara skattningsskalor.

Kan attityder, känslor och upplevelser omvandlas till siffror?

När man mäter och analyserar känslor och upplevelser med kvantitativa metoder (med siffror) använder man ett vetenskapsteoretiskt synsätt som kallas positivism. Man kan rikta kritik mot att omvandla icke lagbundna fenomen som exempelvis känslor och uppfattningar till siffror och statistik (följ gärna föregående länk och läs sidan om vetenskapsteori). Detta är en debatt som i högsta grad fortfarande är levande och det kan vara klokt att vara medveten om det.

Att använda skattningsskalor

Enkäter som försöker mäta upplevelser, åsikter, subjektivt hälsotillstånd, etc. med siffror använder olika former av skattningsskalor. Innan man räknar statistik på skattningsskalor är det en del viktiga val som måste göras:

• Bestäm vad du vill mäta (exempelvis upplevelse av hälsa).
• Vad är syftet? Vill du kunna särskilja mellan individer (som tycker / upplever olika), förutsäga / ge prognos (exempelvis om framtida sjukskrivningsbehov) eller utröna förändring över tid. Här måste du bland annat bestämma om du vill mäta en gång eller titta på förändring mellan två mätningar.
• Finns ett färdigt instrument eller enkät som du kan använda? Om inte måste du själv först konstruera instrumentet / enkäten och se om den mäter det du tror att den mäter. Om du skall konstruera eget instrument / egen enkät är första steget att göra en operationalisering. I det momentet bestämmer du hur frågorna och svarsalternativen skall se ut.
• Bestäm hur insamlade data skall bearbetas. Vilken statistisk metod skall användas? Detta bestäms till största delen av vilka val du gjorde vid operationaliseringen.

Operationalisering

Skall man mäta fenomenet med en enda fråga eller med ett frågeformulär innehållande flera frågor? Fördelar med en enda fråga är att den efterföljande bearbetningen blir enklare. Fördelen med att använda många frågor till samma fenomen är:

• Man kan öka täckningsgraden. Olika individer upplever inte ett fenomen på samma sätt och därmed blir det svårt att beskriva fenomenet med bara en fråga.
• För att få med olika kvaliteter / aspekter på fenomenet.
• För att få fram inom vilken del av fenomenet man ser brister / förbättring / försämring.

Att välja skaltyp

Det finns i princip tre olika skaltyper:

Möjligen är det så att VDS har något bättre test-retest egenskaper än GRS och VAS och att den därför kan vara att föredra.

Likert skala

En speciell typ av verbalt beskrivande skala är Likertskalan. Man ställer ett påstående och svarsalternativen är håller inte alls med eller håller helt med och en del alternativ däremellan. Likertskalan kan ha 3-7 alternativ och det vanligaste är 4-5.

Att välja beteckning av svarsalternativen

VDS och GRS har alltså fasta skalsteg. Det finns ingen given regel på hur många skalsteg man skall ha men varje skalsteg måste ges en egen meningsfull beskrivning, något som sannolikt blir svårt om man överstiger 6-7 skalsteg. VAS har inga fasta skalsteg. Om man använder VDS eller GRS anses det att man vid attitydfrågor bör undvika en mittpunkt, annars är det bra med mittpunkt. När man skall registrera svaren , exempelvis i ett datorprogram, skall svaret kodas till en beteckning. Ibland (vid VDS eller GRS) står beteckningen redan på formuläret som individen / patienten svarar på. Exempel på beteckning av olika svarsalternativ:

Exempel 1, 3, 4 och 5 är alla svarsalternativ med exempel på symboler för en ordningsstruktur utan andra matematiska egenskaper (=ordnad kvalitativ variabel). I exempel nr 4 är alltså 100 bara mer än 10 men inte nödvändigtvis exakt 10ggr så mycket. Exempel nr 2 skulle teoretiskt kunna vara antingen en ordnad kvalitativ eller en diskret kvantitativ variabel. Exempel på sistnämnda skulle kunna vara hur många besök på vårdcentralen har du gjort senaste kvartalet?

Dr Citron’s operationalisering

Dr Citron har nu bestämt sig för att randomisera patienterna till två grupper med C-vitamin eller placebo. Han tänker ge dem en enkät med några frågor om hälsa. Denna enkät får patienterna svara på dels i början och dels efter 6 månader Han bestämmer sig för att alla frågorna blir i form av olika påståenden som de får ta ställning till genom att kryssa i ett av flera fasta alternativ, en så kallad Likertskala enligt VDS (se ovan). (En korrekt operationalisering skall naturligtvis beskriva frågorna och svarsalternativen i detalj men vi gör inte det här med dr Citron’s exempel)

Att mäta och redovisa förändring med skattningsskalor

Om vi återgår till vårt inledande exempel så ville dr Citron mäta förändring. Dr Citron har då tre möjligheter; transitionsfrågor, marginalmodeller och korstabeller. Den sistnämnda är enda alternativet som levererar ett mått (vanligen p-värde) på graden av osäkerhet när man påstår att det verkligen har skett en förändring. Det finns ingen regel som säger att det ena sättet är bättre än det andra.

Transitionsfrågor

Vid slutet av undersökningsperioden ställer man frågor om vilken förändring individen upplever. Exempel på detta kan vara en fråga som återfinns i enkäten SF-36:

Använder man transitionsfrågor finns ingen direkt anledning att fråga initialt. (Däremot kanske man vill ha initiala frågor för att kunna beskriva vilka som inkluderades och hur de mådde då. Använder man vid uppföljningen en transtitionsfråga finns ingen anledning att räkna fram en differens mellan start och uppföljning.

Marginalmodeller

Här visar man grafiskt förändringar över tid. Det finns olika sätt att göra detta på. Ett exempel är genom staplade fraktionsstaplar:

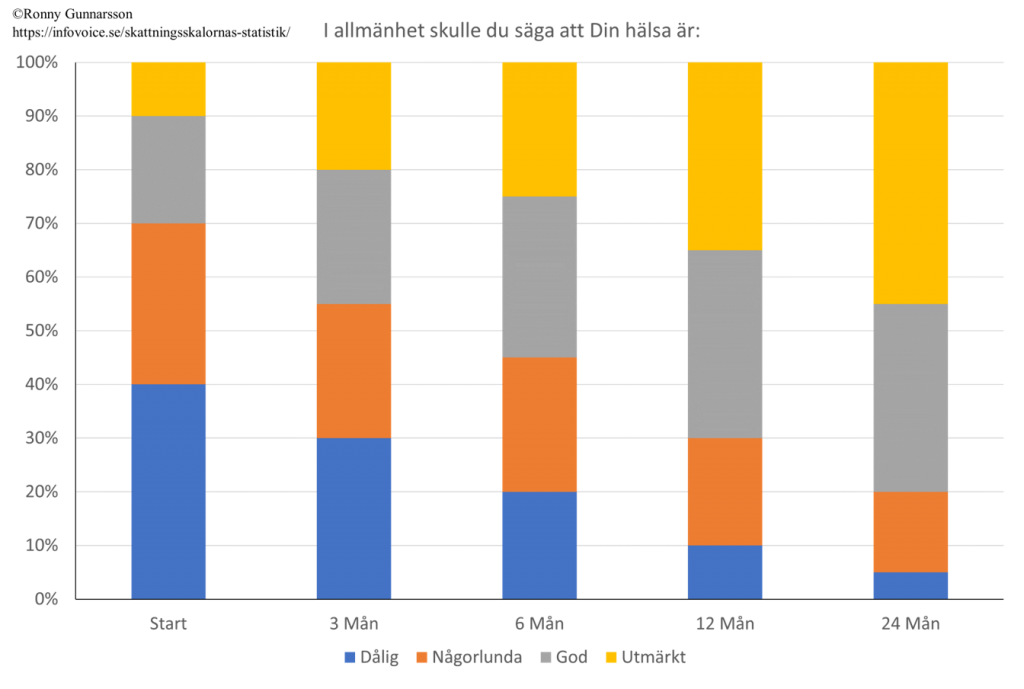
Korstabeller

Här räknar man fram ett mått (vanligen p-värde) på huruvida förändringen ligger inom slumpens felmarginal eller ej. Det finns tre principiellt olika situationer vid denna typ av analys:

• Se om förändringen i en grupp är statistiskt signifikant.
• Se om skillnaden i förändring mellan två matchade grupper är statistiskt signifikant.
• Se om skillnaden i förändring mellan två omatchade grupper är statistiskt signifikant.

Längre ner beskrivs mer detaljerat hur man räknar fram olika mått (oftast p-värden) vid denna typ av jämförande analys.

Analytisk statistik och skattningsskalor

Låt oss anta att dr Citron finner stöd för att C-vitamin sänker blodtrycket. Det är naturligtvis viktigt för effekten att patienten får en bra och positiv information om C-vitamin. Han inleder då en ny undersökning där han vill veta hur patienterna uppfattar informationen. Han ger patienterna personlig information en och en. Direkt efter genomgången får de svara på en fråga:

Samtidigt tar Dr Citron för var och en av konsultationerna och svarar på följande fråga:

Gruppjämförelse

Dr Citron vill veta om män och kvinnor uppfattade situationen olika. svaret på frågan till patienterna analyseras då och han jämför svaren från män och kvinnor. Detta är omatchade grupper. Det finns två alternativ; antingen analyseras data med Mann-Whitney’s test (om vi tar hänsyn till att svarsalternativen har en inbördes ordning – ordinalskala), eller chi-två (om vi väljer att ignorera att svarsalternativen har en inbördes ordning – vi betraktar då data som nominaldata).

Sambandsanalys

Dr Citron vill nu veta, dels om det finns ett samband mellan patientens åsikt och hans egen uppfattning om hur han uppfattade att patienten reagerade.

Det är viktigt att inse att det finns olika typer av samband. Sambandet mellan patienternas skattning och hans egen skattning är graden av överensstämmelse mellan olika bedömningar av en och samma situation. Då passar viktad kappakoefficient (om vi tar hänsyn till att svarsalternativen har en inbördes ordning – ordinalskala) eller kappakoefficient (om vi väljer att ignorera att svarsalternativen har en inbördes ordning – vi betraktar då data som nominaldata).

Gruppjämförelsen som nämndes tidigare gjordes med chi-två. Om vi istället vill se om det finns ett samband mellan kvinnliga respektive manliga patienters uppfattning kan vi göra en sambandsanalys. Grad av överensstämmelse används när samma sak är mätt på olika sätt (som när patient och dr Citron mäter vad som hände i samma konsultation) medan sambansanalys undersöker hur två mätningar av olika fenomen (olika konsultationer) samvarierar. Vi sambandsanalys kan vi här använda Det är då rimligt att använda rangkorrelation (om vi tar hänsyn till att svarsalternativen har en inbördes ordning – ordinalskala) eller Cramer’s phi-koefficient (= Cramer’s V-index) eller rangkorrelation

I den andra frågeställningen där han vill jämföra kvinnor och män så har männen respektive kvinnorna inte skattat samma träff med dr Citron utan var sin egen träff. Sambandet mellan mäns och kvinnors åsikt är då en fråga om samvariation mellan mäns och kvinnors åsikter om likartade (men inte samma) upplevelser. Det är då rimligt att använda Cramer’s phi-koefficient = Cramer’s V-index (om vi väljer att ignorera att svarsalternativen har en inbördes ordning – vi betraktar då data som nominaldata).

Det kan vara av intresse och veta att om vi i den här situationen väljer att ignorera att svarsalternativen har en inbördes ordning (nominaldata) så räknar vi först fram ett chi-två-värde. Därifrån kan vi sedan omvandla chi-två-värdet till antingen ett p-värde, om vi vill fokusera på gruppjämförelse) eller en Cramer’s phi-koefficient. Gruppjämförelser och sambandsanalyser är alltså på något sätt släkt och man kan visa att gruppjämförelser är bara ett specialfall av att göra sambandsanalys. Av detta skälet är det klokt att göra ett försök att förstå vad sambandsanalys är och vad man kan använda det till.

Paradigmkonflikt! Hur gör jag?

Man bör använda en mätskala (och tillhörande statistiska metoder) som passar till typen av variabel. Variabelns mätnivå (vilken mätskala som passar) avgör alltså valet av vilken sorts statistik man skall använda. (Läs gärna vår sida om Variabler som förklarar detta). Det finns emellertid olika åsikter om just skattningsskalor och vilken matematisk mätskala som skall användas. De olika åsikterna kan grupperas i tre huvudinriktningar:

1. En del föreslår att man behandlar skattningsskalorna som vilka siffror som helst, d.v.s. 8 är exakt dubbelt så mycket som 4. Den här åsikten var förr helt dominerande men har numera minskat, framför allt i de Skandinaviska länderna. Fortfarande finns dock ganska många statistiker som menar att detta är korrekt. När det gäller exempelvis VAS är motivet att vid den statistiska analysen analyserar man inte exempelvis smärta utan mm på ett papper. Då är 80 mm på papperet exakt dubbelt som mycket som 40 mm. Först när p-värdet är framräknat och skall tolkas / diskuteras tar man hänsyn till att mm är en representation för något annat, exempelvis upplevd smärta.
2. Den andra huvudinriktningen är att man skall betrakta skattningsskalor som ordinaldata och använda icke parametriska statistiska metoder. Däremot är man inte helt konsekvent när det gäller att utvärdera förändringar. Där tillåter man sig att räkna fram en differens mellan en initial och en uppföljande mätning. Man menar att det är bästa sättet att skilja en stor förändring från en liten förändring.
3. Den sista inriktningen är mest konsekvent och strikt ur matematisk synvinkel. I princip är alla skattningsskalor kategoriska (=kvalitativa) variabler som mäts efter ordinalskalan. Med detta menas att 8 är mer än 4 men inte nödvändigtvis dubbelt så mycket. En konsekvens av detta är att man inte får räkna sumscore, inte får räkna ut ett medelvärde och man får inte räkna fram differenser. Sistnämnda trasslar till det om man vill titta på förändringar över tid mätt med en skattningsskala, exempelvis VAS (Visuell Analog Skala). Man kan alltså inte ta ett slutvärde minus ett initialvärde och använda differensen som den är om variabeln är kvalitativ och mäts enligt ordinalskalan. En variant som anses tillåten är att ta fram en differens och sedan omvandla (transformera) differenserna till “förbättring”, “oförändrad” eller “försämring”. Man kan låta “förbättring” betecknas av +1, “oförändrad” av 0 och “försämring” av -1. Förändringarna har då omvandlats till en ny ordinalskala med tre olika ordnade skalsteg. Vid denna transformering av förändring tappar man information om förändringens storlek.

Huvudinriktning C är teoretiskt mest tilltalande vilket talar för den. Huvudinriktning A kan (i viss mån) försvara sin ståndpunkt teoretiskt. Dessutom tycks huvudinriktning A vara mycket använd internationella vetenskapliga publikationer (framför allt utanför Norden) och en del referee (som granskar din eventuella inskickade artikel) kan vara obekanta med inriktning C. Huvudinriktning B är en kompromiss som egentligen saknar teoretisk grund och som dessutom tycks ha måttligt stöd hos referee (egen erfarenhet). Hur mycket skall man vara “renlärig” (alt C) och är ett acceptabelt pris för renlärigheten att ett bra manuskript blir refuserat? Här finns inga givna svar utan det är viktigt att du själv funderar igenom detta och gör ett val.

En praktisk kompromiss är att ange p-värden framräknade efter alla tre huvudinriktningarna och sedan låta läsaren avgöra. Exempel på publikationer där man använt denna praktiska kompromiss:

• Rosenfeld et al skriver (översatt): “Det finns inget internationellt samförstånd i denna fråga; därför analyseras förändringar i VAS med hjälp av det parametriska ANOVA och det icke-parametriska Friedmanns testet som tillämpas på både råa och transformerade skillnader, även om författarna föredrar det senare”.
  Denna artikel är ett exempel på hur man kan jämföra förändring av smärta (mätt med VAS) mellan omatchade grupper genom att presentera resultatet av beräkningar enligt de tre huvudinriktningarna A-C beskrivna ovan.
  Man ser sedan i första raden i tabell 4 att författarna anger p-värdet för skillnad mellan grupperna i förändring av smärta skattat med VAS på tre sätt enligt A, B och C ovan. Samtliga uträkningar visar ett p-värde <0.05 talande för att man i just denna studien får ungefär samma resultat oavsett hur man räknar, vilket är en styrka.
• Rembeck et al skriver (översatt): “Eftersom det inte finns någon internationell konsensus om hur man kan jämföra förändringar i ordinalskalor mellan grupper använde vi båda de parametriska studenterna testet och det icke-parametriska Mann – Whitney-testet tillämpat på både råa och transformerade skillnader, även om författarna föredrar det senare.”
  Denna artikel är ett exempel på hur man kan jämföra förändring av en attityd (mätt med en enkät bestående av flera frågor) mellan två oberoende grupper genom att presentera resultatet av beräkningar enligt de tre huvudinriktningarna A-C beskrivna ovan. Först togs mått på de olika dimensionerna och en totalpoäng fram enligt enkätinstrumentets manual. Det gjordes enligt huvudinriktning A. Därefter bearbetades förändringsmåtten enligt huvudinriktning A-C beskrivna ovan. Detta sätt att hantera data är alltså inte teoretiskt konsekvent eftersom man valt att följa manualen för enkätinstrumentet trots att manualen baseras på huvudinriktning A.
  Man ser sedan att alla p-värden i tabell 1-3 anger p-värdet för skillnad i förändring mellan grupperna framräknat på tre sätt enligt A, B och C ovan.
• Nordeman et al skriver (översatt): “Eftersom det inte finns någon internationell konsensus om hur man skall jämföra förändringar i ordinalskalor mellan grupper användes både det parametriska t-testet och det icke-parametriska Mann-Whitney-testet som tillämpades på både råa och transformerade skillnader, även om författarna föredrar det senare.”
  Man ser sedan att alla p-värden i tabell 2-3 anger p-värdet för skillnad i förändring mellan grupperna framräknat på tre sätt enligt A, B och C ovan.
• Rindner et al skriver (översatt): “…det finns olika åsikter mellan statistiker om hur man behandlar observationer som mäts med en ordinalskala. Vissa statistiker rekommenderar att man använder parametriska metoder som t-test om observationerna är normalfördelade. Andra säger att ordinaldata alltid måste analyseras med användning av icke-parametriska metoder såsom Mann-Whitneys test. Några statistiker säger också att avsaknaden av likstora (ekvidistanta) skalsteg i ordinalskalan bryter mot grundläggande matematiska krav för att få göra enkla subtraktioner och att en förändring över tiden inte kan beräknas. Således har vi tre möjliga metoder för att analysera data som alla stöds av statistiker men kommer att resultera i olika resultat. För att försäkra oss om att detta val inte leder till fel slutsatser har vi analyserat data med alla tre metoderna.”
  Man ser sedan att alla p-värden i tabell 2 anger p-värdet för skillnad mellan grupperna framräknat på tre sätt enligt A, B och C ovan.

Sumscore?

Många enkäter har delfrågor som sedan skall summeras antingen för att ge ett mått på en högre dimension eller på en total score. Exempelvis så har enkäten SF-36 36 frågor som kan summeras till 8 “dimensioner” (=aspekter) av hälsa och en total score som ger ett totalmått på upplevd hälsa. I princip kan man räkna sin statistik antingen på enskilda frågor, enskilda dimensioner eller på totalpoängen. Hur konstruerar man dimensioner och totalpoäng utifrån svaren på de enskilda frågorna? Här finns olika åsikter. Låt oss åter utgå från de tre huvudinriktningarna nämnda ovan:

1. Skattningsskalorna betraktas som vilka siffror som helst, d.v.s. 8 är exakt dubbelt så mycket som 4. Den här åsikten är fortfarande vanligast i vetenskapliga publikationer. Manualerna till olika enkäter (exempelvis SF-36) bygger oftast på detta sätt att betrakta enkätsvaren. Man räknar då oftast fram sumscore genom att summera svaren från enskilda delfrågor. Teorierna bakom varför man anser sig kunna summera delfrågor diskuteras sällan.
2. Här finns ingen lösning på dilemmat med sumscore. Eftersom huvudinriktning B strävar mot att efterlikna inriktning C men ändå inte bryta för mycket med traditionerna brukar man ofta göra som manualen till enkätinstrumentet säger. Oftast innebär det att man avseende beräkning av dimensioner och globala mått följer huvudinriktning A.
3. Eftersom alla skattningsskalor anses vara ordinaldata utan ekvidistanta skalsteg (8 är mer än 4 men inte nödvändigtvis dubbelt så mycket) får man inte räkna sumscore, inte räkna ut ett medelvärde och man får inte heller räkna fram differenser. Man räknar alltså fram ett mått på en övergripande dimension (aspekt) på annat sätt än med summering av enskilda svar (mer om detta nedan). Teorierna bakom varför man räknar på ett visst sätt presenteras ofta.

Låt oss titta lite mer på huvudinriktning C. Nedan beskrivs några olika situationer och tänkbara lösningsförslag som följer inriktning C när man vill slå samman svaren från flera frågor till en övergripande dimension:

Situation / problem	Lösningsförslag	Exempel
Flera liknade frågor som kan anses vara av lika värde. Frågorna har samma ordinalskala och den har fler än två svarsalternativ	Istället för sumscore låter man medianen för flera frågors utfall representera en dimension . Man får då ett mått på dimensionen utan att behöva summera enskilda frågor.	SF-36 dimensionen Psykiskt välbefinnande (Mental Health, fråga 9b-9d, 9f och 9h).
Flera liknade frågor som kan anses vara av lika värde. Frågorna har ja/nej som svarsalternativ	Antalet ja (eller antalet nej) svar klassificerar individen i A, B, etc, . Man får då ett mått på dimensionen utan att behöva summera enskilda frågor.	a) SF-36 dimensionen Rollfunktion (Role Physical, fråga 4a-4d). Individen klassificeras i A eller B. b) SF-36 dimensionen Social funktion (Social Functioning, fråga 6 och 10). Individen klassificeras i A-E.
Två olika inte direkt likvärdiga frågor som tillsammans skall avspegla en dimension	Istället för sumscore görs en tabell där tänkbara svarsalternativ på ena frågan bildar kolumner och tänkbara svarsalternativ på andra frågan bildar rader . I de olika rutorna anger man en värdering av de tänkbara kombinationerna.	a) SF-36 dimensionen Smärta (Bodily Pain, fråga 7 och 8) där man kan gradera A-G. b) SF-36 dimensionen Social funktion (Social Functioning, fråga 6 och 10) där man kan gradera A-F.
Flera frågor som avspeglar en stegring	Frågorna kan ordnas efter hur mycket varje fråga försöker beskriva, exempelvis av fysisk funktion. Första frågan där man får svar på en fysisk begränsning blir värdet för den övergripande dimensionen .	SF-36 dimensionen Fsykisk funktion (Physical Functioning, fråga 3a-3j).

Ovanstående tabell är lättare att förstå om du läser Svenssons artikel . Huvudinriktning C räknar inte fram en total sumscore (global hälsa) för SF-36. Det är svårt att hävda att de åtta olika dimensionerna i SF-36 är likvärdiga och därmed saknas grund för att ange medianen mellan dem som mått på global hälsa. Däremot kan man räkna fram ett globalt mått för enkäten EuroQoL som bara består av 5 frågor och två dimensioner och ändå vara trogen alternativ C . Orsaken till detta är att bara två dimensioner kan behandlas på samma sätt som man räknar fram dimensionen smärta i SF-36 (se tabellen ovan).

Att välja statistisk metod vid skattningsskalor

Utifrån hur man ser på vad skattningsskalorna representerar räknar man sedan med lämplig statistisk metod (se tabell nedan). Här krävs lite eftertanke. Nedan beskrivs tänkbara strategier beroende på vad du vill ha fram och beroende på om du vill använda huvudinriktning A, B eller C. Det bör betonas att det kan finnas olika åsikter om nedanstående och undertecknad gör inte anspråk på att ha sanningen i denna fråga.

	Huvudinriktning A	Huvudinriktning B	Huvudinriktning C
Gruppjämförelse: Jämföra enstaka mätning mellan två omatchade grupper	Jämför grupperna med parametriskt test (exempelvis Student’s t-test för två omatchade grupper)	Jämför grupperna med icke parametriskt test (exempelvis Mann-Whitney´s test = Rangsummetest = Wilcoxon two unpaired samples)	Jämför grupperna med icke parametriskt test (exempelvis Mann-Whitney´s test = Rangsummetest = Wilcoxon two unpaired samples)
Gruppjämförelse: Jämföra enstaka mätning mellan två matchade grupper	Räkna fram differensen mellan de två individerna inom paret. Använd parametriskt test (exempelvis Student’s t-test för matchade grupper) för att se om medelvärdet för differenserna inom paret skiljer sig statistiskt signifikant från 0.	Räkna fram differensen mellan de två individerna inom paret. Använd icke parametriskt test (exempelvis Wilcoxon one sample signed rank sum test = Teckenrangtest) för att se om differenserna inom paret skiljer sig statistiskt signifikant från 0.	Ta fram en skillnad inom paren. Koda skillnaden i varje par så att du får tre alternativ; förändrade åt ena hållet (individen i grupp A förbättras mer än individen i grupp B), förändrade åt andra hållet (B bättras mer än A) respektive oförändrade (ingen skillnad inom paret). Räkna icke parametriskt test (Teckentest) för att se om antalet där A>B skiljer sig statistiskt signifikant från antalet där A<B. … … eller … … Använd en metod framtagen av professor Elisabeth Svensson och ytterligare beskriven och exemplifierad av Sonn & Svensson .
Gruppjämförelse: Jämföra förändring i en grupp. Eventuellt med ett fast (förväntat) värde. Det förväntade värdet sätts ofta till 0 (=ingen förändring).	Räkna fram differensen. Använd parametriskt test (exempelvis Student’s t-test för ett stickprov) för att se om medelvärdet för differensen skiljer sig statistiskt signifikant från 0.	Om det förväntade värdet är 0 föreslås följande: Räkna fram differensen. Använd icke parametriskt test (exempelvis Wilcoxon one sample signed rank sum test = Teckenrangtest) för att se om differenserna skiljer sig statistiskt signifikant från det förväntade värdet.	Om det förväntade värdet är 0 föreslås följande: Räkna fram differensen mellan mätning 1 och 2 för varje individ. Koda om differenserna till förändrade åt ena hållet (förbättrade?), förändrade åt andra hållet (försämrade?) respektive oförändrade. Räkna icke parametriskt test (Teckentest) på de omkodade differenserna för att se om antalet individer som förbättrats skiljer sig statistiskt signifikant från antalet som försämrats. … … eller … … Använd en metod framtagen av professor Elisabeth Svensson och ytterligare beskriven och exemplifierad av Sonn & Svensson .
Gruppjämförelse: Jämföra förändring mellan två omatchade grupper	Räkna fram differensen för varje individ. Använd parametriskt test (exempelvis Student’s t-test för två omatchade grupper) för att se om medelvärdet för differenserna skiljer sig statistiskt signifikant mellan grupperna.	Räkna fram differensen. Använd icke parametriskt test på differenserna (exempelvis Mann-Whitney´s test = Rangsummetest = Wilcoxon two unpaired samples) för att se om förändringen i grupperna skiljer sig åt.	Räkna fram differensen mellan mätning 1 och 2 för varje individ. Koda om differenserna till förändrade åt ena hållet (förbättrade?), förändrade åt andra hållet (försämrade?) respektive oförändrade. Förslagsvis kodar du förbättrade som +1, oförändrade 0 och försämrade -1. Räkna icke parametriskt test (exempelvis Mann-Whitney´s test = Rangsummetest = Wilcoxon two unpaired samples) på de omkodade differenserna.
Gruppjämförelse: Jämföra förändring mellan två matchade grupper	Räkna fram differensen för varje individ. Räkna sedan fram differensen mellan de två förändringarna inom paret. Använd parametriskt test (exempelvis Student’s t-test för matchade grupper) för att se om medelvärdet för differenserna inom paret skiljer sig statistiskt signifikant från 0.	Räkna fram differensen för varje individ. Räkna sedan fram differensen mellan de två förändringarna inom paret. Använd icke parametriskt test (exempelvis Wilcoxon one sample signed rank sum test = Teckenrangtest) för att se om differenserna inom paret skiljer sig statistiskt signifikant från 0.	Räkna fram differensen för varje individ. Koda om differenserna till förändrade åt ena hållet (förbättrade?), förändrade åt andra hållet (försämrade?) respektive oförändrade. Förslagsvis kodar du förbättrade som +1, oförändrade 0 och försämrade -1. Nu skall du ta fram en skillnad inom paren (se nedan). Koda skillnaden i varje par så att du får tre alternativ; förändrade åt ena hållet (individen i grupp A förbättras mer än individen i grupp B), förändrade åt andra hållet (B bättras mer än A) respektive oförändrade (ingen skillnad inom paret). Räkna icke parametriskt test (Teckentest) på skillnaderna för att se om antalet par där A förbättras mer än B skiljer sig statistiskt signifikant från antalet där B förbättras mer än A.
Analys av samvariation: Samvariation mellan två skattningsskalor	Jämför svars utfallet mellan de två skattningarna med Pearson’s korrelationskoefficient	Jämför svars utfallet mellan de två skattningarna med Spearman´s rangkorrelationskoefficient	?
Analys av likhet: Visa likhet mellan två skattningsskalor	Här skulle nog de flesta statistiker välja kappakoefficient för att jämföra svars utfallet mellan de två skattningarna. Några få skulle kanske välja Intra Class Correlation (=ICC).	Jämför svars utfallet mellan de två skattningarna med kappakoefficient.	Jämför svars utfallet mellan de två skattningarna med kappakoefficient. … … eller … … Använd en metod framtagen av professor Elisabeth Svensson och ytterligare beskriven och exemplifierad av Sonn & Svensson .

Som nämns i högra kolumnen ovan har professor Elisabeth Svensson tagit fram en metod för att analysera parade ordinaldata . I situationen när vi vill studera förändring i en grupp över tid finns enligt huvudinriktning C två alternativ. Den ena är teckentest och den andra är “Svenssons metod”. Skillnaderna mellan dessa två metoder kan beskrivas som:

	Teckentest	“Svenssons metod”
Tar hänsyn till storleken av förändringen	Nej, d.v.s man ignorerar viss insamlad information	Ja, d.v.s. man kan utnyttja informationen bättre
Ger ett mått på gruppens förändring	Ja, i form av ett p-värde	Ja, i form av ett RP-värde som kan variera mellan -1 till +1. Om RV är 0 har ingen ändring skett. (RP = Relative Position)
Ger ett mått på individernas spridning från gruppens förändring	Nej	Ja, i form av ett RV-värde som kan variera mellan 0 och 1. Lågt värde indikerar att individernas förändring inte spretar ut så mycket från trenden i gruppen. (RV = Relative rank-Variance).
Exempel där 371 patienter skattas med “ADL staircase” flera gånger under ett antal år. Vid en analys där man tittar på förändringen under en 6-års period framkommer att: 115 har försämrats i ADL-funktion, 250 är oförändrade och 6 har förbättrats – figur 2a i Sonn och Svenssons artikel från 1997 .	Antalet patienter som har försämrats är fler än antalet som har förbättrats (p<0,0000001).	RP=0,061 (med medelfelet 0,015) RV=0,0021 (med medelfelet 0,00085)
Sannolikhet att en granskare / refereé hos en vetenskaplig tidskrift förstår analysmetoden	Mycket stor eftersom teckentestet är väl känt sedan tidigare.	Låg sannolikhet eftersom denna metod fortfarande är mindre känd och dess originalpublikationer är svåra att få tag i.

Vilket är bäst att använda vid parade ordinaldata? Teckentest eller “Svenssons metod”? Det finns inget givet svar. Båda metoderna har sina fördelar och nackdelar. Du får välja själv och därefter måste du kunna försvara ditt val.

Några fler praktiska exempel

• Se om förändringen i en grupp är statistiskt signifikant:
  Detta är samma som i tabellen ovan kallas “Jämföra enstaka mätning i en grupp med fast (förväntat) värde”. Här jämför man varje individs slutvärde och initialvärde. Skiljer sig differenserna från det förväntade värdet 0 (d.v.s. ingen förändring)? Vi väljer att följa huvudinriktning C ovan och väljer alternativet teckentest. Då räknar man inte direkt ut en differens utan tittar bara på om de överhuvudtaget har förändrats och i så fall åt vilket håll. Låt oss anta att dr citron gav 63 individer C-vitamin. Han frågade alla i början och efter ett år “I allmänhet, hur skulle du vilja säga att din hälsa är?” De fördelade sig då så att 37 angav efter ett år ett bättre värde, 22 var oförändrade och 4 angav ett sämre värde. Man kan nu göra teckentest eller McNemars test. I Båda dessa test ignorerar man de 22 som blev oförändrade. Gör vi teckentestet får vi att p= 0.0000001. Det vill säga att gruppen som helhet har förbättrats och förbättringen förklaras inte av slumpen. Sannolikheten att vi har fel när vi påstår detta är en på tio miljoner.
• Se om skillnaden i förändring mellan två matchade grupper är statistiskt signifikant:
  Här matchar man ihop individer parvis. Vi antar att Dr Citron har parat ihop ett antal patienter utifrån kön och ålder. Den ena i paret slumpas till placebo och den andra till C-vitamin. Vi följer åter inriktning C beskriven ovan. När undersökningsperioden är slut tar man fram antalet par där de som fick C-vitamin har förbättrats mer än de som fick placebo samt tvärtom. Paren som förändrades lika bortser man ifrån. Man räknar sedan på samma sätt som i ovanstående exempel, d.v.s. med teckentest eller McNemars test.
• Se om skillnaden i förändring mellan två omatchade grupper är statistiskt signifikant:
  I detta exempel antar vi att dr Citron hade en omatchad kontrollgrupp som fick syrliga karameller (beträffande utseende och smak var dessa lika C-vitaminet). Vi följer åter inriktning C beskriven ovan. Patienterna får svara på enkät dels initialt och dels en tid senare efter “behandling”. Resultatet blev enligt följande:

	C-vitamin	“Placebo”
Förbättrade	37	29
Oförändrade	22	26
Sämre	4	8

Eftersom det finns en viss ordning mellan förbättrade, oförändrade och försämrade bör man jämföra förändringen mellan dessa två grupper med Mann-Whitney’s test och inte chitvå (chi-square) som ju bortser från ordningen. Skulle man i en situation få att inga blev oförändrade (inte så ovanligt om man tittar på förändringar i VAS) så gör man ändå Mann-Whitney’s test. Beträffande ties och små stickprov så läs mer om detta på sidan om Mann-Whitney’s test.

Referenser