Ronny Gunnarsson. "Korrelation och regression" [on INFOVOICE.SE]. Available on: https://www.infovoice.se/korrelation-och-regression/. Information was retrieved July 18, 2025.
| Suggested pre-reading | What this web page adds |
|---|---|
| This web-page provides an introduction to regression and correlation. Reading this will give you an introduction and overview of these concepts necessary to understand more (on following pages going into more details). |
Korrelation och regression handlar om att försöka beskriva verkligheten i olika matematiska formler. Vilken matematisk formel kan bäst beskriva verkligheten? Det finns olika matematiska modeller. De vanligaste modellerna är linjära modeller där man försöker hitta en räta linjens ekvation som kan beskriva verkligheten. Oftast handlar det om hur en variabel (låt oss för enkelhets skull kalla den y ändras när en eller flera andra variabler (som vi brukar kalla x) ändras. Se denna enkla introduktion av Jens:
Nedan ser du en eller flera bilder. Att klicka på en bild tar dig till YouTube där videon spelas upp. Youtube’s hemsida kommer då att lagra “kakor (cookies)” på din dator. Du kan läsa mer om detta på vår sida om GDPR och “kakor (cookies)”.

Korrelation
Introduktion till korrelation
Korrelation handlar om hur väl två olika variabler samvarierar. Vi kan för enkelhets skull kalla variablerna för y och x. Varje markering anger värdet för y respektive x för varje observation (Figur 1). Här ser vi att om x är högre är det sannolikt att också y är högre.
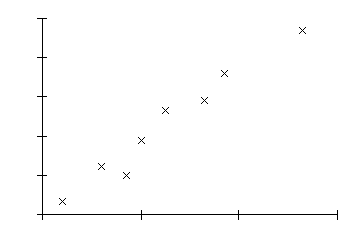
Man talar nästan alltid om linjär korrelation, det vill säga man ser hur väl samvariationen mellan dessa två variabler liknar en rät linje. Man kallar denna linjen regressionslinje (Figur 2).
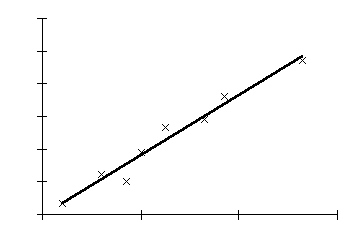
Korrelationskoefficient
Vid korrelationsanalys räknar datorn fram en korrelationskoefficient (=r). Den berättar hur nära ett linjärt samband vi har i vårt stickprov. Om korrelationskoefficienten ligger nära noll finns inget linjärt samband (men det kan finnas ett icke linjärt samband). Ju mer koefficienten avlägsnar sig från noll desto starkare linjärt samband. Som mest kan koefficienten avlägsna sig från noll till +1 eller -1. Vid +1 finns ett perfekt linjärt samband som är positivt, d.v.s. när x ökar så ökar även y. Vid en korrelationskoefficient nära -1 gäller omvänt, d.v.s. när x ökar så minskar y. I figur 2 ovan ser vi att vårt stickprov ligger ganska nära vår regressionslinje. I det exemplet blir korrelationskoefficienten 0,98 vilket antyder ett starkt linjärt samband.
Nu kan man ju fundera på vad korrelationskoefficienten hade blivit om vi bara haft två kryss i diagram 1 och 2. Låt oss leka med tanken på att vi behåller kryssen med det lägsta respektive högsta x-värdena. Om vi sedan förbinder dessa två x (som kanske representerar två patienter) ser vi att linjen mellan dem passar perfekt, d.v.s. inget kryss ligger utanför regressionslinjen (Figur 3).
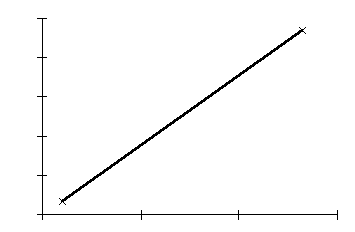
I figur 3 blir korrelationskoefficienten 1,0. Räcker det verkligen med endast två mätvärden (två patienter) för att kunna säga att det föreligger ett perfekt linjärt samband mellan två variabler???
Hypotesprövning av korrelation
Vi kan betrakta vår framtagna regressionslinje som en hypotes. Hypotesen är alltså att verkligheten liknar vår regressionslinje. Nu skall vi testa om hypotesen är korrekt. Eftersom sanningen inom statistiken inte är svart-vit innebär det att med ett p-värde skatta osäkerheten i vår hypotes. Detta gör vi genom att göra en hypotesprövning av vår korrelationskoefficient. Det finns tabeller där man kan se vilket p-värde som vår korrelationskoefficient motsvarar. I tabellen behöver man veta korrelationskoefficienten och antalet undersökta individer. Utifrån dessa två fakta ger tabellen ett p-värde. datorprogram levererar dessa p-värden automatiskt.
I vårt första exempel (Figur 1+2) med en korrelationskoefficient på 0,98 och med 8 undersökta individer så blir p-värdet <0,001. Vi skulle kunna påstå att sambandet mellan variabeln x och y hos de 8 undersökta individerna kan beskrivas med en rät linje och sannolikheten att vi har fel när vi påstår detta är <0,1% (eller mindre än 1 på 1000). I vårt nästa exempel (Figur 3) med en korrelationskoefficient på 1,0 och med 2 undersökta individer så blir p-värdet 1,0. Detta innebär att osäkerheten i vårt påstående, att sambandet mellan variabeln x och y kan beskrivas med en rät linje, är maximal.
Regression
Olika typer av regression beroende på antal variabler
En eller flera variabler betecknas som “beroende variabler”. Med det menas att de tänks vara beroende av och ändras när en eller flera oberoende variabler ändras. Man talar om olika typer av regression beroende på om man har en eller flera beroende respektive oberoende variabler :
- Simple regression: En beroende och en oberoende variabel
- Multivariable regression = multiple regression: Mer än en oberoende variabel
- Multivariate regression: Mer än en beroende variabel
- Multivariate multivariable regression: Mer än en beroende variabel samt dessutom mer än en oberoende variabel.
Linjär regression
Introduktion till linjär regression
Den vanligaste och enklaste matematiska modellen man använder är en rät linje. Om man bara har en oberoende variabel (bara ett x) så är formeln för denna linje:
y = a + ßx
vilket ibland skrivs som:
y = ß0 + ß1x
men i Sverige oftast som:
y = a + bx
(man kan även skriva det på annat sätt men det fördjupar vi oss inte i här)
I formeln är y en variabel (exempelvis kroppslängd) och x är en annan variabel (exempelvis ålder). a och b är konstanter, d.v.s. fasta tal. Värdena på a och b bestämmer hur linjen ser ut. Konstanten a brukar kallas för intercept och b för regressionskoefficient. Linjen / formeln kan sedan användas för att förutsäga värdet på y om man vet x. Vi skulle exempelvis kunna förutsäga medelvärdet för längden på 12-åriga flickor om vi hade de exakta värdena på a och b. Villkoren för att få göra sådana förutsägelser (prediktioner) är att:
- det finns ett linjärt samband mellan y och x
- vi håller oss inom de intervall av x-värden som har studerats och befunnits ha ett linjärt samband med y. Exempelvis kan det vara så att kroppslängd och ålder har ett linjärt samband mellan 4-12 års ålder men utanför det åldersintervallet är inte sambandet linjärt (med samma värden på a och b)
Man kan låta en dator ta fram värden på a och b och på så sätt beskriva en formel för linjärt samband mellan två variabler, x och y, oavsett om det faktiskt finns ett linjärt samband mellan dessa variabler eller ej. Det är alltså viktigt att veta om det verkligen finns ett linjärt samband. Detta tar man reda på genom att:
- Titta på data med ett scatterdiagram
- Om scatterdiagrammet anbtyder ett linjärt samband gär en korrelationsanalys.
Att ta fram en regressionslinje
Vanligt är att man börjar med att rita upp hur de två variablerna ligger i förhållande till varandra med ett scatterdiagram (Figur 1 ovan). Värdet på variabeln x och värdet på variabeln y möts i ett kryss. I ett sådant diagram är varje kryss en patient (om det nu är patienter som blev undersökta). Därefter ritar man in en linje som ser ut att passa för att beskriva sambandet mellan variabeln y och variabeln x (Figur 2 ovan).
Linjen (som brukar kallas regressionslinje) kan ju dras lite olika. Vilken linje är den som bäst beskriver sambandet mellan x och y? Den vanligaste metoden för att avgöra vad som är den bästa linjen kallas minsta kvadratmetoden.
Man kan tänka sig en mängd olika linjer för att beskriva sambandet mellan x och y. Var och en av dessa linjer kan testas. Man tar då för varje punkt/kryss (för varje patient om det är patienter som är undersökta) kvadraten på skillnaden mellan punktens/kryssets y-värde och den tänkta linjens y-värde. Orsaken till att differenserna kvadreras är för att bli av med problemet att ungefär hälften av differenserna ligger över noll och ungefär hälften under noll (ett fåtal kan hamna på exakt noll). Differenserna kallas ofta för residualer. Alla dessa kvadrerade differenser (residualer) summeras och resultatet kallas SSE (Sum of the squared errors). SSE kallas även residualkvadratsumma (= Sum of squared residuals). Den linje som ger minst SSE är den bästa.
Hypotesprövning av regressionskoefficienten
När vi tar fram vår matematiska modell (vår linje) så är ju den konstruerad ur ett stickprov. Våra framräknade värden på konstanterna a och b är alltså skattningar. Verkligheten (den stora population som stickprovet togs ur) kanske ser lite annorlunda ut. För att skatta osäkerheten kan man ta fram standardavvikelse och räkna fram konfidensintervall för a respektive b.
Ett annat sätt är att göra en hypotesprövning. Vi betrakta vår framtagna regressionslinje som en hypotes. Det är egentligen flera hypoteser som ryms i en enkel linjär regression:
- Att verkligheten överhuvudtaget kan liknas vid en rät linje.
- Att regressionskoefficienten är som vi tror.
- Att interceptet är som vi tror.
Hur man testar den första hypotesen har vi beskrivit under rubriken ovan som heter “Hypotesprövning av korrelation”. Olika statistikprogram kan räkna fram ett p-värde som ett mått på sannolikheten att vi har fel när vi påstår att regressionskoefficienten respektive interceptet har ett visst värde.
Determinationskoefficient
Determinationskoefficienten (=r2=r^2=R2) är en koefficient som anger hur stor del av variationerna i den beroende variabeln (y) som kan förklaras av variationer i den oberoende variabeln (x) under förutsättning att sambandet mellan x och y är linjärt. Determinationskoefficienten kallas ofta förklaringsgrad.
Man räknar fram determinationskoefficienten genom att ta kvadratsummorna för regressionsmodellen (Regression/Model – Sum of squares) delat med den totala kvadratsumman (Total – Sum of squares). Vid enkel linjär regression kan determinationskoefficienten även räknas fram genom att kvadrera korrelationskoefficienten (r).
I vårt första exempel (Figur 1+2) blir determinationskoefficienten 0,98 i kvadrat, d.v.s. 0,96. Det innebär att 96% av variationen i y kan förklaras av ändringar i x. Resterande 4% är oförklarade, d.v.s. beror på annat som vår matematiska modell inte kan förklara. Determinationskoefficienten har en tendens att öka ju fler oberoende variabler (ju fler olika x) vi lägger in i vår matematiska modell. Samtidigt innebär fler x även en osäkerhet att vi får in skensamband ger oss en falskt hög R2. Det finns ett korrigerat R2 som tar hänsyn till detta. Det kallas för ra^2 eller “adjusted R-square”. Koefficienten ra^2 minskar därför ofta ju fler oberoende variabler (x) man lägger till i sin matematiska modell.
Den beroende variabeln och olika typer av linjär regression
- Standard linear regression: Den beroende variabeln mäts med en intervall eller kvotskala.
- Logistic regression: Den beroende variabeln är nästan alltid binär / dikotom (det finns undantag vid “ordinal logistic regression” när den beroende variabeln mäts med en ordinal skala).
- Cox regression: Den beroende variabeln består av två variabler: en som anger om händelsen av intresse har inträffat (kodas ofta som 1) eller inte (kodas ofta som 0). Den andra variabeln anger tiden en individ har följts upp oavsett om händelsen har inträffat eller ej.
Översikt över olika typer av linjär regression
| Simple regression | Multivariable regression = multiple regression | Multivariate regression | Multivariate multivariable regression | |
|---|---|---|---|---|
| Standard linear regression | Simple standard linear regression = Unadjusted standard linear regression | Multivariable standard linear regression = multiple standard linear regression = adjusted standard linear regression | Factor analysis | Factor analysis |
| Logistic regression | Simple logistic regression = unadjusted logistic regression | Multivariable logistic regression = multiple logistic regression = adjusted logistic regression | Multivariate probit regression (bivariate probit regression is a special case with two dependent variables) | Multivariate multivariable probit regression |
| Proportional hazards regression = Cox regression | Simple proportional Hazards regression | Multivariable proportional Hazards regression / multiple proportional hazards regression | ? | ? |
Multipel linjär regression
Ekvationen för en enkel regressionslinje har bara hade en oberoende variabel (bara ett x). Man kan tänka sig en matematisk modell där man vill beskriva hur y varierar beroende på hur flera andra variabler (flera x) varierar. Man får då en multipel regressionsmodell och den principiella formeln för detta är:
y = a + b1x1 + b2x2 + b3x3 …..e.t.c.
Här har vi ett intercept (a) och flera regressionskoefficienter (flera olika b). Den enkla regressionen kan enkelt åskådliggöras med ett scatterdiagram (Figur 1+2). En regression med två oberoende variabler kan åskådliggöras med ett tredimensionellt (svårförståeligt) diagram. Regressioner med tre eller fler oberoende variabler kan inte åskådliggöras i diagramform.
I en multipel regression har vi flera oberoende variabler (flera x). Hur många x skall tas med i modellen? Vi kanske har gjort en studie där vi har samlat in en stor mängd olika variabler. Skall alla dessa användas? Det kanske är flera hundra!
Det bästa är att ha en rimlig teori om vilka variabler som skall inkluderas. Om detta saknas får man göra en “fishing expedition”, d.v.s låta datorn undersöka alla tillgängliga variabler och vaska fram de mest betydelsefulla. De vanligaste alternativen när man låter datorn välja är:
- All possible regressions
- Forward selection
- Backward elimination
- Stepwise regression
- Lasso regression
(Detta avsnitt är under konstruktion. Vi beklagar olägenheten.)
Icke-linjär regression
Det är inte ovanligt att man vid en enkel linjär regressionsanalys finner att korrelationskoefficienten är låg och icke signifikant. Det faktum att vår korrelationskoefficient inte är statistiskt signifikant innebär inte att verkligheten inte kan beskrivas med en matematisk modell. Om vår linjära modell inte passar så kanske en icke linjär modell gör det. Det finns många olika varianter på icke linjära modeller, exempelvis polynomapproximationer. Om man har endast en oberoende variabel (ett x) är det är fel att inte först titta på sambandet mellan x och y i ett scatterdiagram innan man gör sin regressionsanalys. Låt oss anta att vi gör en enkel linjär regression (Figur 4).
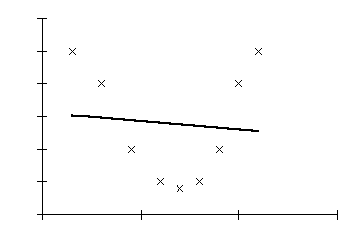
(=polynomapproximation av 1:a graden)
Om vi ber datorn göra en linjär regressionsanalys med y som beroende variabel och x som oberoende spottar datorn ur sig följande formel:
y = 3,097 – 0,2566x
Vi finner en korrelationskoefficient på 0,094 (determinationskoefficient 0,0089) och p-värdet för korrelationskoefficienten blir högt (1,0). Även om formeln ovan ser vacker och förtroendeingivande ut är den alltså helt värdelös. Istället för att ge upp kan man prova andra matematiska modeller (Figur 5).
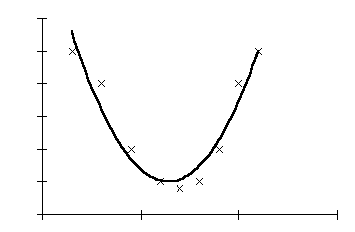
Figur 5 ger exempel på hur samma stickprov kan beskrivas med en andragradsekvation som matematiskt är:
y = 8,818 – 12,191x + 4,753x2
När vi övergår från en enkel linjär regression till en polynomregression av andra graden ökar förklaringsgraden (determinationskoefficienten) från 0,0089 till 0,9285. Vi har nu en matematisk modell som mycket bättre förklarar verkligheten. Man kan prova och se om man hittar andra matematiska modeller som ännu bättre beskriver verkligheten (diagram 6).
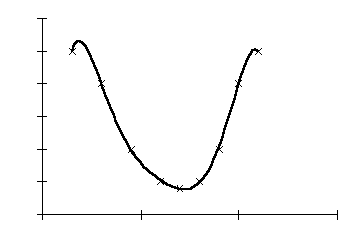
Figur 6 ger exempel på hur samma stickprov kan beskrivas med en sjättegradsekvation. Formeln för en polynomregression av 6:e graden är principiellt:
y = a + b1x – b2x2 + b3x3 – b4x4 + b5x5 – b6x6
och i exemplet (Figur 6) blir det:
y = – 9,6853 + 111,71x – 303,44x2 + 383,01x3 – 254,3x4 + 85,798x5 – 11,512x6
När vi övergår från en polynomapproximation av andra graden till en polynomregression av sjätte graden ökar förklaringsgraden (determinationskoefficienten) från 0,9285 till 0,9997. Vi har nu en matematisk modell som ännu bättre förklarar verkligheten.
Allt det här låter ju bra. Låt oss alltid använda 6:e gradens polynomapproximationer! Problemet med de här avancerade matematiska konstruktionerna är att de är svåra att tolka. Erfarenheten säger att många mätbara biologiska samvariationer liknar ganska hyfsat linjära ekvationer, åtminstone så länge man håller sig inom rimliga gränser, helst inom de värden på x som är undersökta.
Den allt övervägande delen av matematiska modeller som används (>95%?) är linjära modeller. Ibland används andra modeller och vanligast är då logaritmiska modeller och därnäst polynomapproximationer av andra graden. Det är ytterst ovanligt i medicinska sammanhang att man använder mer komplicerade modeller.
Det bör påpekas att icke linjära modeller är avancerad statistik och kräver i regel medverkan av statistiker.
Vidareläsning
Referenser
Ronny Gunnarsson. "Korrelation och regression" [on INFOVOICE.SE]. Available on: https://www.infovoice.se/korrelation-och-regression/. Information was retrieved July 18, 2025.

