Evaluation of dichotomous diagnostic tests
Revised: 2001-11-10

A test to diagnose a disease caused by a microbiologic agent usually has a dichotomous outcome: presence or no presence of the etiologic agent. A fundamental prerequisite for its usefulness is that a test designed to detect a bacterium can detect this bacterium better than if the doctor made a guess based on a preliminary clinical observation. In some situations the doctor’s guess of viral or bacterial etiology is not much more accurate than setting the diagnosis by flipping a coin. When can it be expected that the test provides more information than a random choice? In order to answer this question the test may be described by means of sensitivity and specificity, or by various indices such as the Youden index¹, the efficiency², the index of validity¹ or kappa³. The Youden index is dependent on sensitivity and specificity while indices of validity and efficiency are also dependent on the prevalence of disease. Thus they are more informative than the Youden index. The disadvantage of all the indices is that they do not differentiate between the outcome growth of bacteria (T+) or no growth of bacteria (T-). In some tests T- may be highly relevant but T+ of little value. An example of this is the outcome of throat cultures in children (as will be shown later in this dissertation). However, likelihood ratios or predictive values consider T+ and T- separately.

Likelihood ratios depend on sensitivity and specificity alone. Since predictive values also depend on the prevalence of disease they yield more information concerning the evaluation of bacterial cultures than likelihood ratios. The positive likelihood ratios provide information about how much more the odds, for the phenomena the tests is design to detect, increases in case of a positive test. Likelihood ratios cannot be used in clinical practice unless you know the pre-test odds or pre-test probability. The positive predictive value (PPV) provides you with the probability of the phenomenon the test is design to detect.

Although predictive values seem to be the ideal measure of a test it does not take into consideration the presence of symptomatic carriers (individuals harboring the agent our test is supposed to detect and at the same time ill by something else, usually a virus). Methods that may consider asymptomatic carriers are relative risk and hypothesis testing.

Sensitivity and specificity

In order to evaluate a test, sensitivity and specificity are most often used^1,4-5. They are calculated by comparing the observed test outcome with the outcome of the gold standard in a sample of n subjects: 

 The sensitivity is mathematically independent of the disease prevalence. However, if the test is a microbiologic diagnostic test, in situations with a low disease prevalence, every test will probably be examined less carefully compared to a situation with a higher disease prevalence. Thus, a decrease in the disease prevalence might reduce the sensitivity of the test. A well-known effect on the sensitivity is seen by altering the cut off limit for considering the test as positive, an issue of great interest for manufacturers of rapid tests for detection of GABHS. These phenomena can be studied by constructing Receiver Operating Characteristic curves (ROC-curves). As long as the disease prevalence is below 50%, the influence of the disease prevalence on the sensitivity is small⁶.

It could be appropriate to say that the sensitivity and the specificity inform you about the health status of your test rather than the health status of your patient⁴. Therefore, there is also a need for another method to evaluate throat and nasopharyngeal culture.

Youden's index

As a measure of a tests efficiency Youden in 1950 suggested an index (J)¹: 

J = Sensitivity + Specificity – 1

This index does not take into account the prevalence of disease and therefore it contains less information than index of validity or efficiency. The Youden index is rarely used.

Index of validity and efficiency

One way of characterizing a diagnostic test is to calculate the proportion of correctly classified individuals as an index of validity (Iv).

If the sensitivity and the specificity are equal, then Iv is independent of the disease prevalence¹. In all other situations, Iv depends on both the sensitivity, the specificity and the prevalence of disease¹. The efficiency is the same as Iv multiplied by 100 and expressed in per cent².

Kappa

The index of validity is the probability of agreement between the test and the gold standard. Kappa is a modification of the index of validity. It compares the found agreement with the agreement that would be expected by chance. To understand the concept, kappa is calculated in an example. In the example a rapid test to detect GABHS is evaluated with conventional throat culture as the gold standard⁷:

Thus, the index of validity was 0.895, which means that 89.5% of the cases had been correctly classified by the rapid test. Does this indicate that the rapid test is a useful test? By using kappa a better answer may be provided. To calculate kappa the found index of validity is compared to the index of validity that could be expected if our gold standard and the rapid test worked independently. This means that 26.7% (28/105) of the gold standard tests and 20% (21/105) of the rapid tests will be positive, but that there is no correlation between the outcome of the two tests. Thus, the two tests will only have the same outcome by chance, not because their outcomes are correlated. The probability for both tests to be positive will then be 0.267´0.2=0.0534. The expected number of samples with a positive outcome in both the gold standard and the rapid test is 0.0534´105=5.607. The table may now be completed under independence between the gold standard and the rapid test:

How much better is an index of validity of 0.895 compared to an index of 0.640? Kappa is designed to answer this question. Kappa (k) is the ratio between the improvement by using our test (0.895-0.640) and the possible scope for doing better than chance (1-0.640). In our example kappa is 

This could be considered as good agreement between our test and the gold standard³. The most common use of kappa is to evaluate inter-rater agreement between different measures of the same event.

A serious disadvantage with indices, like Youden’s index, index of validity, efficiency and kappa, is that they do not distinguish between T+ and T-. It may often be found that one of the two possible outcomes is informative but not the other. This makes index of validity or efficiency less appropriate as methods for evaluating throat and nasopharyngeal cultures.

Likelihood ratio

How much better is our test than flipping a coin? Likelihood ratios are one method to provide this information. The likelihood ratios give us information about how much the disease probability has changed because of the test results. The formulae for positive likelihood ratio (PLR) and negative likelihood ratio (NLR) are

    and  

Likelihood ratios of a positive and negative test when flipping a coin are both 1; indicating that the pre-test odds for disease have not been altered by the test. The higher the likelihood ratio of a positive test, the more information will be obtained by a positive test. If the likelihood ratio of a negative test gets close to zero it will yield much more information than flipping a coin. As seen from the formulae above likelihood ratios are solely depending on sensitivity and specificity, and thus they are measures of the health status of your test. Thus, a high PLR does not necessary indicate that a positive test indicates presence of disease⁸. However, it can be shown that in case of a positive test

 Thus, likelihood ratios will provide clinically valuable information if you know the pre-test odds for disease. You may then use likelihood ratios to calculate post-test odds which easily can be transformed into post-test probability for disease.

Predictive value of a test

The sensitivity, the specificity, all of the different test indexes mentioned above and the likelihood ratio do not solve the clinical diagnostic problem⁴. These statistical methods provide information of the health status of the test, but not the health status of our patients. In the doctor-patient situation the doctor wants to know the probability of disease in the patient. If the pre-test probability for the bacterial disease is known, then the post-test probability for this disease may be calculated using the likelihood ratio.

An early description of a formula that may be used for direct calculation of post test probability of disease was published in 1763 and is frequently refereed to as the Bayes’ theorem⁹. Bayes’ theorem can be formulated as

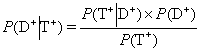
P(×) denotes the probability of the condition within parenthesis, i.e. P(D+) denotes the probability of disease (= prevalence of disease = pre-test probability of disease) and P(T+) the probability of the event of getting a positive test result. P(…½…) is the probability of the event indicated before the vertical bar if the conditions stated after the bar is fulfilled. P(T+½D+) is the probability of a positive test result in patients having the disease, i.e. sensitivity. Bayes’ theorem is often transformed to 

P(D+½T+) is often named the positive predictive value (PPV). There is a corresponding negative predictive value (NPV) predicting the absence of disease in case of a negative test result expressed as

It is easier to understand the predictive values if their calculation is compared with the calculation of the sensitivity and the specificity.

PPV always increases with increasing disease prevalence¹⁰. PPV is mainly affected by the specificity and the prevalence of the disease¹⁰. As long as the sensitivity and the specificity are reasonably high, their effect on NPV is negligible. A low prevalence of disease will, if the sensitivity and specificity is reasonably high, result in a high NPV. Increasing the prevalence of disease will only have minimal effect on the NPV until the prevalence of disease reaches a high proportion¹⁰.

For a better understanding, the flipping of a coin may illustrate the relation between sensitivity, specificity and predictive values. A common misconception is to equate flipping a coin with a predictive value of 50%¹¹. By flipping a coin, there is a 50% chance that heads will come up (bacterial disease) or tails (viral disease); thus the sensitivity and the specificity are both 50%. Hence the predictive values of flipping a coin depends on the disease prevalence¹¹. In the situation with the coin, the PPV will be the same as the disease prevalence and positive + negative predictive value will be 100%. If the disease prevalence is high, then it is possible to achieve a high PPV by flipping a coin and with low disease prevalence flipping a coin will yield a high NPV.

The concept of predictive values has gradually become more common. It is well established that the predictive values in most clinical situations provide more useful information on how to assess the clinical value of a test than sensitivity and specificity alone^4,8,10,12-15.

The event that is being predicted when applying the concept of predictive values to the situation of evaluating throat and nasopharyngeal cultures is the presence of potentially pathogenic bacteria and not if the patient is ill from the potentially pathogenic bacteria isolated! Not all patients with a positive test for presence of potentially pathogenic bacteria have a bacterial infection. Some of these patients may be just symptomatic carriers of these potentially pathogenic bacteria with a concomitant viral infection. These patients may be misclassified as having an infection caused by the potentially pathogenic bacteria isolated. If the symptomatic carriers suffer from viral infections, antibiotic treatment should usually be avoided. Thus, the clinical value of microbiological testing is related to the prevalence of symptomatic carriers among the patients.

If symptomatic carriers exist and should be treated differently from patients ill from the etiologic agent, then the predictive values of the test is not good enough.

Relative risk

Symptomatic carriers of potentially pathogenic bacteria are common in many patients suffering from a respiratory tract infection. In such cases there is a need of a test evaluation method that involves information about the carriers. The concept of relative risk (RR) could be useful when comparing the outcome of the test in one population with the outcome of the test in another population¹⁶. When using RR there is no need for a gold standard. RR is thus defined as the increased risk in one study group compared to the risk in another group, for instance patients compared to healthy individuals:

If we want to elucidate the relation between a risk factor and a disease we usually perform a case-control study. In a case control study it would be more appropriate to use odds ratio. However, in this case the disease is the risk factor for having a positive test so this situation more resembles a historical cohort study where relative risk is appropriate. Since the subjects of interest are chosen with regard to certain characteristics, such as the presence or absence of a respiratory tract infection, as opposed to the test outcome, then RR is a better choice than odds ratio¹⁶.

Hypothesis test of two independent groups

Another possibility is to utilize information about asymptomatic carriers by comparing the prevalence of bacteria found in patients with healthy individuals. To compare proportions between two independent groups, Chi-square with or without Yates’ correction could be useful. Fisher’s exact test should be used in case of small numbers. The outcome of the hypothesis testing is a p-value and, p<0.05 indicates that the bacterium may be involved as an etiologic agent.

Conclusions

A summary and further conclusions are made in the next page The choice between different evaluation methods.

References

1. Taube A. Sensitivity, specificity and predictive values: a graphical approach. Stat Med 1986;5:585-91.
    
2. Galen RS, Gambino RS. How to determine the predictive value and efficiency of a test when reading a scientific paper. Beyond normality: The Predictive value and efficiency of medical diagnoses. New York: John Wiley & sons; 1975, pp 29-40.
    
3. Altman DG. Some common problems in medical research. Practical statistics for medical research. London: Chapman & Hall; 1991, pp 396-439.
    
4. Begg CB. Biases in the assessment of diagnostic tests. Stat Med 1987;6:411-23.
    
5. Begg CB. Advances in statistical methodology for diagnostic medicine in the 1980's. Stat Med 1991;10:1887-95.
    
6. Brenner H, Gefeller O. Variation of sensitivity, specificity, likelihood ratios and predictive values with disease prevalence. Stat Med 1997;16:981-91.
    
7. Andersen JS, Borrild NJ, Renneberg J. An evaluation of a commercial co-agglutination test for the diagnosis of group A streptococcal tonsillitis in a family practice. Scand J Prim Health Care 1992;10:223-5.
    
8. Altman DG. Diagnostic tests. Practical statistics for medical research. London: Chapman & Hall; 1991, pp 409-19.
    
9. Bayes RT. An Essay toward solving a problem in the doctrine of chance. Philo Trans Roy Soc 1763;53:370-418.
    
10. Vecchio TJ. Predictive value of a single diagnostic test in unselected populations. N Engl J Med 1966;274:1171-3.
     
11. Galen RS, Gambino RS. Appendix III Standard error of a percentage. Beyond normality: The Predictive value and efficiency of medical diagnoses. New York: John Wiley & sons; 1975, pp 129.
     
12. Sackett DL, Haynes BR, Guyatt GH, Tugwell P. The interpretation of diagnostic data. In Clinical Epidemiology, a basic science for clinical medicine. Sackett DL, Haynes BR, Guyatt GH, Tugwell P. Boston: Little, Brown and Company 1991, pp69-152.
     
13. Fong DS, Seddon JM. Diagnostic tests: an overview. Int Ophthalmol Clin 1994;34:187-95.
     
14. Altman DG, Bland JM. Diagnostic tests 2: Predictive values. BMJ 1994;309:102.
     
15. Valenstein PN. Evaluating diagnostic tests with imperfect standards. Am J Clin Pathol 1990;93:252-8.
     
16. Altman DG. Comparing risks. Practical statistics for medical research. London: Chapman & Hall; 1991, pp 266-71.

Ronny Gunnarsson MD PhD
Department of Primary Health Care
Göteborg University
SWEDEN

Back to Main menu