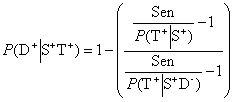
Formulae for EPV
Revised: 2001-10-28
This section explains the formulae necessary to calculate etiologic predictive value (EPV). The simplest way to perform the calculation is to use our calculator found in the menu to the left (if you do not see a menu to the left click on "Back to Main menu" at the bottom of this page).
The doctor usually want to predict the presence of a specified disease (D), for example throat infection caused by the agent , among patients with similar symptoms (S) caused by various etiologic agents. The symptoms, for example a sore throatand fever, are similar for different etiologic agents. However, the treatmentmight be very different depending on the etiologic agent. To make a good prediction, a test (T) is often used, for example a throat culture, to detect the presence of a marker (M), for example GABHS, associated with the disease (D). Let T+ indicate a positive test and T- a negative one. Let M+ indicate the presence of the marker, for example GABHS, and M- absence. Let D+ indicate the presence of the disease the doctor wants to predict, for example throat infection caused by GABHS, and D- absence. The populationD- may have symptoms, as long as the symptoms are not caused by GABHS. To predict disease caused by GABHS, information from a group of healthy individuals (S-) can be used and the outcome could be compared to that of a group of symptomatic patients (S+). The healthy control population and the population of patients have to be comparable in respect to confounding factors like age. The patients whose illness is caused by our marker will be described as S+D+, and thus, the patients ill from something else than the marker M will be described as S+D-. An appropriate term for the population S+D- could be symptomatic carriers. In this situation it is appropriate to use P( | ) for the probability of the event indicated before the vertical bar if the conditions stated after the bar are fulfilled. Positive EPV(PEPV) is defined as P(D+|S+T+) and negative EPV (NEPV) as P(D-|S+T-). For these two predictive values it can be shown that, under reasonable assumptions, the following expressions are valid:
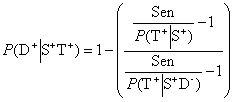
Formula 1 Positive EPV

Formula 2 Negative EPV
where Sen is the sensitivitywith which the test T discovers the marker M, i.e.
![]()
The step by step construction of formula 1 and 2 is shown in a dissertation (found in the section "Key references" in the menu to the left)
Interval estimate of EPV
When estimating sensitivity and specificityit is appropriate to present an interval estimate [1, 2]. This is rarely done in articles on evaluating diagnostic tests [2]. The precision of predictive values, just as in the case with sensitivity and specificity, is dependent on the size of our sample [2]. It is therefore also appropriate to use some kind of interval estimate for predictive values. Some methods for calculating an interval estimate of predictive values exist but they require a gold standard identifying disease or a previously known prevalence of disease [2, 3]. Both prerequisites may sometimes be difficult to achieve. If previously known prevalence is used the study combines results of independent studies. This might be questionable if the prevalence of the specified disease varies in time and geographical location.
It can be shown that, confidence limits for the positive etiologic predictive value are (compare with Formula 1 above)
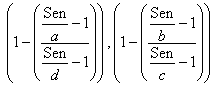
Formula 3 Confidence interval for PEPV
and that confidence limits for the negative etiologic predictive value are (compare with Formula 2 above)
![]()
Formula 4 Confidence interval for NEPV
The step by step construction of these formulae is shown in a dissertation (found in the section "Key references" in the menu to the left)
Estimating EPV from samples
Next step is to explain how to estimate positive and negative etiologic predictive values from samples. The expressions (Formula 1) and (Formula 2) contain the three probabilities
Sen, P(T+|S+), P(T+|S+ D-)
as well as
P(T-|S+), and P(T-|S+ D-)
Here each of the last two probabilities is the complement of one of the three first, so therefore only the three first require consideration.
Since Sen has nothing to do with the disease D, one may assume Sen to be known from previous experience. The probability P(T+|S+) is estimated using test results from symptomatic patients. A small p denotes an estimate of P and N(Χ) denotes the number of persons with (Χ):
![]()
Formula 5 Probability of a positive test in patients
The remaining probability, P(T+|S+D-), requires careful consideration. It is not possible to differentiate patients with throat pain caused by GABHS(S+D+) from symptomatic carriersill by another agent (usually a virus) but carrying GABHS (S+M+D-). Thus, no scientific study to date has been able to estimate P(T+|S+D-) in our example with throat infection. The relation between the two probabilities may be described as
![]()
Formula 6 Probability of a positive test in patients ill from another cause
where the factor θ in most situations can be assumed to be 1. Further aspects of θ are presented in the FAQ-area (in the menu to the left). The probability P(T+|S-), is estimated using test results from healthy individuals:
![]()
Formula 7 Probability of a positive test in healthy individuals
By using the expressions (Formula 5 - Formula 7) the probabilities needed to estimate EPV(in Formula 1 and Formula 2) can easily be calculated.
Concerning the estimation of the confidence limits for EPV, the values a, b, c and d are calculated by taking the output from the formulae (Formula 5) and (Formula 7) and inserting it into Formula 8 - Formula 11:
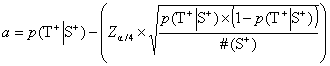
Formula 8 Lower confidence limit for positive tests in patients
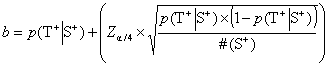
Formula 9 Upper confidence limit for positive tests in patients
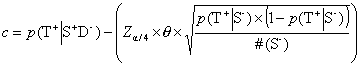
Formula 10 Lower confidence limit for positive tests in patients ill from another cause
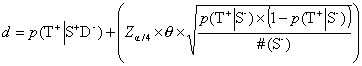
Formula 11 Upper confidence limit for positive tests in patients ill from another cause
To obtain a confidence intervalfor EPVwith a confidence level of at least 0.95 let
![]()
When a, b, c, and d are calculated, confidence limits for EPV may be calculated by using formula 3 and formula 4.
Ronny Gunnarsson MD
PhD
Department of Primary Health Care
Gφteborg University
SWEDEN