Why not use likelihood ratio?
 Revised: 2001-10-28

Question: How is positive etiologic predictive value different from using positive likelihood ratio to predict post-test probability for disease if one compensates for the presence of carriers? Could it be that using LR with adjusted pre-test probability for disease makes Etiologic Predictive Value unnecessary?

Consider the following example: A conventional throat culture has been obtained during a summer period from 36 children of age 3-15 years having a sore throat possibly caused by group A beta-hemolytic streptococci (GABHS)1. Among those 36 cultures a throat culture indicated presence of the bacterium GABHS in 11 (31%).

However, some of the children might be ill due to a virus as well as carrying GABHS. To investigate this phenomenon we may collect data from healthy children. During the same period of time throat cultures were obtained from 290 healthy children of age 3-15 living in the same geographical area, and showing no signs indicating possible GABHS-caused tonsillopharyngitis1. Among those 290 cultures a throat culture indicated presence of GABHS in 37 (13%).

How well does the outcome of the throat culture predict whether the sore throat is caused by the bacterium GABHS? Let us compare three different approaches to this question:

  1. Ignore the importance of carriers and calculate a prediction (Predictive Values) of presence of GABHS in the throat.
     
  2. First compensate for carriers by altering pre-test probability for disease and then use likelihood ratios (LR) to calculate a prediction of the disease a sore throat caused by GABHS.
     
  3. Use Etiologic Predictive Values (EPV) to compensate for carriers and calculate a prediction of the disease a sore throat caused by GABHS.

1. Ignoring carriers

If the sensitivity of throat culture to find presence of GABHS in the throat is assumed to be 90%2, 3, 4, 5, 6, 7 and the specificity to be 97%5, 6 then the predictive values in respect of presence of GABHS in the throat are estimated so (see also Appendix 1):

Table I - Calculating predictive values
(PPV=Positive predictive value, NPV=Negative predictive value)
 

Gold standard

  
 

GABHS
 (M+)

No GABHS
 (M-)

  

Positive test (T+)

10.26

0.74

11

Negative test (T-)

1.14

23.86

25

 

11.40

24.60

36

PPV = 10.26/11 = 93.3%

NPV = 23.86/25 = 95.4%
(M denotes a Marker. In this case the marker is GABHS. One must also remember that the purpose of these calculations is to elucidate differences between different statistical approaches. In reality it would of course be difficult to have 10.26 individuals. If we round the numbers to avoid parts of individuals we get PPV 90.9% and NPV 96.0%).

2. First compensate for carriers, then use LR

Calculate likelihood ratios
If sensitivity (Sen.) and specificity (Spec) are known then positive and negative likelihood ratio of a throat culture can be calculated. In the above example they are:


 

If pre-test probability for disease, P(D+), is known then post-test probability for disease may be calculated if the likelihood ratio is known. This is done by first transforming pre-test probability for disease to pre-test odds for disease, O(D+). Post-test odds for disease is then calculated as follows:


 

Finally post-test odds for disease is transformed to post-test probability for disease.

Compensating for carriers - two suggestions
 In our example 30.6% of the children with a sore throat had growth of GABHS. At the same time 12.8% of healthy children had growth of GABHS. Let us see what happens if we compensate for this by altering the pre-test probability for disease. (We will later discuss if it is appropriate to do this). Two different suggestions have been made concerning this adjustment. The first is to assume that pre-test probability for disease can be calculated by taking the probability for a positive test in patients, P(T+|S+), minus the probability for a positive test in a healthy control group without any symptoms like a sore throat, P(T+|S-), i.e.

The other suggestion is similar but instead of comparing test outcome the focus is on the probability for presence of GABHS among patients, P(M+|S+), and the probability for presence of GABHS in a healthy control group, P(M+|S-), i.e.

Compensating for carriers - using probability for a positive test
 Let us try the first suggested way to compensate the pre-test probability for disease. The pre-test probability for disease will then be 30.6%-12.8% = 17.8%. In this suggestion it corresponds to a pre-test odds of


 

The post-test odds for disease in case of a positive test would be 30:4.62 and the corresponding post-test probability for disease


 

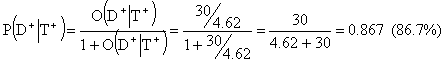
The post-test odds for disease in case of a negative test would be 0.103:4.62 and the corresponding post-test probability for disease is


 

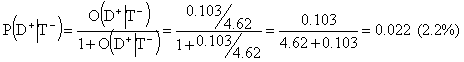
Here 2.2% is the probability for disease if test is negative. The common negative predictive value, P(D-|T-), is the probability for absence of disease in case of a negative test. Thus, N-PV is 100%-2.2%=97.8%.

Compensating for carriers - using probability for presence of a marker
 Let us now try the second suggested way to compensate the pre-test probability for disease. As mentioned above this suggestion is

We can find P(M+|S+) in Table I (+Appendix 1) and P(M+|S-) in Appendix 2.


 

This corresponds to a pre-test odds of


 

The post-test odds for disease in case of a positive test will then be 30:3.88 and the corresponding post-test probability for disease is


 

The post-test odds for disease in case of a negative test will then be 0.103:3.88 and the corresponding post-test probability for disease is


 

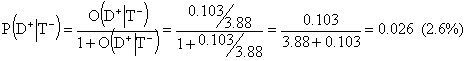
Here 2.6% is the probability for disease if test is negative. The common negative predictive value, P(D-|T-), is the probability for absence of disease in case of a negative test. Thus, N-PV is 100%-2.6%=97.4%.

 3. Compensate for carriers with EPV

As mentioned on other pages EPV will compensate for carriers. In the above mentioned example positive EPV is 67.9% and negative EPV is 96.7%.

Comparison between approaches

As we can see (Table II) the different approaches will yield quite different post-test probability for disease.

Table II - Post-test probabilities for the disease a sore throat caused by GABHS if the test a throat culture is positive and post-test probabilities for absence of this disease if test is negative:
(Numbers from example described above)
  Positive test Negative test
  1. Without compensating for carriers:
 93.3% 95.4%
  1. Using LR
    Compensating with Test outcome:
    Compensating with presence of M:
 86.7%
88.5%		 97.8%
97.4%
  1. Compensating for carriers using EPV:
 67.9% 96.7%

It is easy to understand that if we ignore carriers we will have a higher positive predictive value than if we consider carriers. However, it is interesting to see that in our example (Table II) compensating for carriers by using LR yields a much higher positive predictive value than using EPV. To understand this we must clarify the situation.

We can look at the relation between test outcome and presence or absence of the etiologic agent (Table III).

Table III - Relation between test outcome (T+, T-) and presence (M+) or absence (M-) of specified bacterium in patients having a sore throat
  A sore throat caused by....
  ....GABHS (D+) ....other than GABHS (D-)
  GABHS present
(M+)		 (GABHS not present)
(M-)		 GABHS present
(M+)		 GABHS not present
(M-)

Positive test (T+)

 True positive ----- True positive False positive

Negative test (T-)

 False negative ----- False negative True negative

Since the disease is caused by M then M must be present in the patient at some stage of the disease. Thus, the second column will have no patients (se also the page defining markers).

We can also look at the relation between test outcome and the presence or absence of disease (Table IV).

Table IV - Relation between test outcome (T+, T-) and presence (D+) or absence (D-) of specified disease  in patients having a sore throat
  A sore throat caused by....
  ....GABHS (D+) ....other than GABHS (D-)
  GABHS present (GABHS not present) GABHS present GABHS not present

Positive test (T+)

 True positive ----- False positive* False positive

Negative test (T-)

 False negative ----- True negative** True negative
*The positive test does not represent true disease (D+) and is therefore considered to be false positive. However, it indicates that the patient is a carrier of GABHS.

**Although the patient carry GABHS a negative test will correctly identify the patient as not having the disease, thus being (D-).

Table III and IV differ in the third column. This difference is important and will have implications. Thus, we have to consider if bacteria are present, test performance like sensitivity and specificity as well as the difficult question of whether the symptoms are caused by the present bacterium or not.

Using LR, as in the second approach, is incorrect because:

a In using LR we use an incorrect value for PLR and NLR
LR is calculated from sensitivity and specificity. In our example the sensitivity (0.9) and specificity (0.97) are calculated in previous studies using gold standards that detects presence of a bacteria, not presence of the disease a sore throat caused by GABHS. If we had a gold standard predicting this disease (which we do not have) then sensitivity and specificity of a throat culture to detect disease could be calculated. This sensitivity and specificity to detect disease would be different, and most probably the specificity would be lower than 0.97. A lower specificity would result in a lower PLR and a higher NLR. Thus, in using LR we use an incorrect value for PLR and NLR resulting in an overestimation of post-test probability for disease, P(D+|T+) and an overestimation of probability for absence of disease in case of a negative test, P(D-|T-). The error will have greater impact on the estimation of P(D+|T+).
   
b In using LR we use an incorrect value for pre-test probability
We need a pre-test probability for disease, P(D+), if we want to use LR to estimate post-test probability for disease, P(D+|T+). To estimate P(D+) we must consider all patients ill from something else than GABHS (D-). Using P(T+), or P(M+), among patients minus P(T+), or P(M+), among healthy individuals to estimate P(D+) is wrong (this is explained in the next section). This error will result in an underestimation of both P(D+|T+) and P(D-|T-). The error will have greater impact on the estimation of P(D+|T+) compared to the estimation of P(D-|T-).

As we can see the two errors will affect the outcome in opposite directions. However, in our example error a seems to have a greater influence than error b.

Estimating pre-test probability for disease

It has been suggested that pre-test probability for disease can be estimated by reducing the proportion of positive tests in patients with the proportion of positive tests found among healthy individuals. This approach could be expressed as

An alternative would be to reduce the probability for patients harboring the etiologic marker with the probability for healthy individuals carrying the etiologic marker. This approach could be described as

We will take our example with children having a sore throat and see what happens if we apply these methods of calculating pre-test probability for disease. By doing some calculations (explained in the Appendix 3 at the bottom of this page) our example presented previously can be presented with actual numbers (Table V).

Table V - Relations between test outcome (T+, T-), presence (M+) or absence (M-) of GABHS and presence (D+) or absence (D-) of the disease a sore throat caused by GABHS
  A sore throat caused by....  
  ....GABHS (D+) ....other than GABHS (D-)  
  GABHS present
(M+)		 (GABHS not present)
(M-)		 GABHS present
(M+)		 GABHS not present
(M-)		  

Positive test (T+)

 7.45 0 2.81 0.74 11

Negative test (T-)

 0.83 0 0.31 23.86 25
  8.28 0 3.12 24.60 36

The first suggested approach is that we take the proportion of positive tests among all patients (11/36=30.6%) minus the proportion of positive tests in a healthy control population (37/290=12.8%). This results in a pre-test probability for disease that is 17.8%.

The secondly suggested approach means that we in patients with a sore throat take the probability for harboring a marker (11.4/36=31.7%) minus the probability for healthy children being a carrier of the etiologic marker (32.5/290=11.2%). This results in a pre-test probability for disease that is 20.5%.

However, none of these two estimations is a correct estimation of the pre-test probability for disease P(D+) which is 8.28/36=0.23 (23%) (data from Table V). The error of using a lower P(D+) will provide a lower predictive value of a positive test than if the correct  P(D+) was used.

Estimating post-test probability for disease

We can also see (Table V) that the prediction for the disease a sore throat caused by GABHS would be 7.45/11=0.677 (67.7%) and the prediction for absence of this disease in case of a negative test would be (0.31+23.86)/25=0.967 (96.7%). The small difference between these predictions and the positive and negative EPV presented previously (Table II) has two explanations:

a Rounding numbers produce a small error. Using many decimals in every step of the calculation would minimize this problem.
   
b In the calculations in Appendix 3 and Table V we assumed specificity to be 0.97. This estimation is done in previous studies and may not be exactly the same when the test is applied to our patients. EPV does not need an estimate of specificity. However, if we want to calculate according to Appendix 3 we can try different estimates for the specificity to find the estimate that results in the same prediction as EPV. By doing so we have made an estimation of the specificity the test appears to have among our patients.

Using many decimals in every step of the calculation in Appendix 3 and using the specificity 0.9472 would yield a positive prediction for the disease a sore throat caused by GABHS of 67.865% and a negative prediction of 96.682% which is exactly the same result as positive and negative EPV.

It is better to use EPV than the calculations presented in Appendix 3 and Table V because EPV does not need an assumed value of the specificity. Every additional assumption that is needed is also an additional uncertainty.

Other WebPages of interest

Other pages with subjects that might be of interest is:

(You can click on these links to quickly see the pages)

References

  1. Gunnarsson, R.K., Holm, S.E. and Söderström, M. `The prevalence of beta-haemolytic streptococci in throat specimens from healthy children and adults. Implications for the clinical value of throat cultures' , Scand J Prim Health Care, 15, 149-155 (1997).
     
  2. Centor, R.M., Meier, F.A. and Dalton, H.P. `Throat cultures and rapid tests for diagnosis of group A streptococcal pharyngitis' , Ann Intern Med, 105, 892-899 (1986).
     
  3. Kaplan, E.L. Unresolved problems in diagnosis and epidemiology of streptococcal infection. Streptococci and Streptococcal diseases, Academic Press, New York. 1972. pp 557-570.
     
  4. Stillström, J., Schwan, A. and Björklind, A. `Streptococcal throat infection: calculation of test standards and a comparison between an antigen detection test and culture' , Scand J Prim Health Care, 9, 149-154 (1991).
     
  5. White, C.B., Harris, R., Weir, M.R., Gonzales, I. and Bass, J.W. `Streptococcal pharyngitis. Comparison of latex agglutination and throat culture' , Clin Pediatr (Phila), 27, 431-434 (1988).
     
  6. Lewey, S., White, C.B., Lieberman, M.M. and Morales, E. `Evaluation of the throat culture as a follow-up for an initially negative enzyme immunosorbent assay rapid streptococcal antigen detection test' , Pediatr Infect Dis J, 7, 765-769 (1988).
     
  7. Christensen, P., Danielsson, D., Hovelius, B. and Kjellander, J. `Preliminary identification of beta-hemolytic streptococci in throat swab cultures with a commercial blood agar slide (streptocult)' , J Clin Microbiol, 15, 981-983 (1982).

Appendix 1

Assuming that a throat culture has a sensitivity of 0.9 and a specificity of 0.97 then our example with children having a sore throat may be described (Table VI).

Table VI - Relation between T and M among patients
  GABHS present
(M+)		 (GABHS not present)
(M-)		  

Positive test (T+)

0.9 x A

0.03 x B

11

Negative test (T-)

0.1 x A

0.97 x B

25

 

A

 B

36

We can see that

Formula 1

and also that

Formula 2

If we replace A in formula 2 with formula 1 we get

As we know B then the remaining cells in Table VI is easily calculated and we end up with Table I.

Appendix 2

As in Appendix 1 we may in a similar way describe the situation for the healthy children mentioned in our example (Table VII).

Table VII - Relation between T and M among healthy individuals
  GABHS present
(M+)		 (GABHS not present)
(M-)		  

Positive test (T+)

0.9 x A

0.03 x B

37

Negative test (T-)

0.1 x A

0.97 x B

253

 

A

 B

290

As in Appendix 1 we find that

and also that

As in Appendix 1 we may now calculate all numbers and the result is

Table VIII - Relation between T and M among healthy individuals
  GABHS present
(M+)		 (GABHS not present)
(M-)		  

Positive test (T+)

29.25

7.72

37

Negative test (T-)

3.25

249.8

253

 

 32.5 257.5

290

Appendix 3

In the previously presented example we assumed sensitivity to be 0.90 and specificity to be 0.97. Thus we know that

Table IX - Relation between test outcome (T+, T-), presence (M+) or absence (M-) of GABHS and presence (D+) or absence (D-) of the disease a sore throat caused by GABHS
  Illness/symptoms caused by....  
  ....GABHS (D+) ....other than GABHS (D-)  
  GABHS present
(M+)		 (GABHS not present)
(M-)		 GABHS present
(M+)		 GABHS not present
(M-)		  

Positive test (T+)

 0.9 x Y 0 0.9 x X 0.03 x Z 11

Negative test (T-)

 0.1 x Y 0 0.1 x X 0.97 x Z 25
  Y 0 X Z 36

It is easy to see that all positive tests among the patients with a sore throat may be described as

Formula 3

and all tests may be described as

Formula 4

Furthermore if we assume that the proportion of positive tests in healthy individuals (12.8%) are the same as the proportion of positive tests among patients with a sore throat caused by a virus we find that

Formula 5

Formula 5 may be rearranged

Formula 6

Let us insert formula 6 into formula 3

Formula 7

Let us replace X in formula 4 with formula 7 and Z with formula 6

Formula 8

Let us replace X in formula 8 with formula 7

As we now know Y we can use formula 7 to calculate X and then Z is calculated using formula 4. When we know Y, X and Z the rest is easily calculated.

Ronny Gunnarsson MD PhD
Department of Primary Health Care
Göteborg University
SWEDEN

Back to Main menu